4.3 The Mean Value Theorem and Monotonicity
We have taken for granted that a function \(f(x)\) is increasing if \(f'(x)\) is positive and decreasing if \(f'(x)\) is negative. In this section, we prove this rigorously using an important result called the Mean Value Theorem (MVT). Then we develop a method for “testing” critical points—that is, for determining whether they correspond to local minima or maxima.
The MVT says that a secant line between two points \((a, f(a))\) and \((b, f(b))\) on a graph is parallel to at least one tangent line in the interval \((a, b)\) [Figure 4.23], assuming that \(f(x)\) is differentiable between \(a\) and \(b\) and continuous on \([a,b]\). Because two lines are parallel if they have the same slope, what the MVT claims is that there exists a point \(c\) between \(a\) and \(b\) such that
\[ \underbrace{f'(c)}_{\text{Slope of tangent line}} = \underbrace{\frac{f(b) - f(a)}{b-a}}_{\text{Slope of secant line}} \]
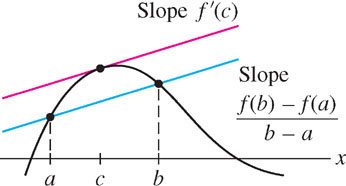
THEOREM 1 The Mean Value Theorem
Assume that \(f(x)\) is continuous on the closed interval \([a, b]\) and differentiable on \((a, b)\). Then there exists at least one value \(c\) in \((a, b)\) such that
\[ \boxed{f'(c) = \dfrac{f(b) - f(a)}{b-a}} \]
Rolle’s Theorem (Section 4.2) is the special case of the MVT in which \(f(a) = f(b)\). In this case, the conclusion is that \(f'(c) = 0\).
GRAPHICAL INSIGHT
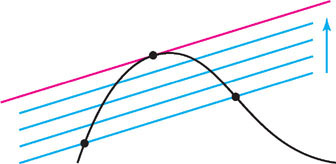
Imagine what happens when a secant line is moved parallel to itself. Eventually, it becomes a tangent line, as shown in Figure 4.24. This is the idea behind the MVT. We present a formal proof at the end of this section.
227
CONCEPTUAL INSIGHT
The conclusion of the MVT can be rewritten as
\[ \boxed{f(b) - f(a) = f'(c)(b-a)} \]
We can think of this as a variation on the Linear Approximation, which says
\[ f(b) - f(a) \approx f'(a)(b - a). \]
The MVT turns this approximation into an equality by replacing \(f'(a)\) with \(f'(c)\) for a suitable choice of \(c\) in \((a, b)\).
EXAMPLE 1
Verify the MVT with \(f(x)=\sqrt{x}\), \(a = 1\), and \(b = 9\).
Solution First, compute the slope of the secant line (Figure 4.25):
\[ \frac{f(b) - f(a)}{b-a}=\frac{\sqrt{9} - \sqrt{1}}{9-1} = \frac{3-1}{9-1} = \frac{1}{4} \]
We must find \(c\) such that \(f'(c) = \frac{1}{4}\). The derivative is \(f'(x)=\frac{1}{2}x^{-\frac{1}{2}}\), and
\[ f'(c) = \frac{1}{2\sqrt{c}} = \frac{1}{4}\implies 2\sqrt{c} = 4\implies c=4 \]
The value \(c = 4\) lies in \((1, 9)\) and satisfies \(f'(4)=\frac{1}{4}\). This verifies the MVT.
Question 4.6 Mean Value Theorem and Monotonicity Progress Check 1
phPtXhnDIRAz7WmQp1LvldmMKHdzZBkubtNEXwoI+/P8VwlCqa0sOgkVE+HnP+7qApIJRn7sWVtiOxrgi51XdhM111/Nx1tjqwy5tVoQPfx+ig2rCtLwCpOCCVvSMiRFzlgsKZX38FsPB7AMfkFzhcKizQgKqtXGohyXTb6/C4xMxE+1OK+SgVvnmcg=As a first application, we prove that a function with zero derivative is constant.
COROLLARY
If \(f(x)\) is differentiable and \(f'(x) = 0\) for all \(x \in (a, b)\), then \(f(x)\) is constant on \((a, b)\). In other words, \(f(x) = C\) for some constant \(C\).
Proof
If \(a_{1}\) and \(b_{1}\) are any two distinct points in \((a, b)\), then, by the MVT, there exists \(c\) between \(a_{1}\) and \(b_{1}\) such that
\[ f(b_{1}) - f(a_{1}) = f'(c)(b_{1} - a_{1}) = 0\quad\text{(since \(f'(c) = 0\))} \]
Thus \(f(b_{1}) = f(a_{1})\). This says that \(f(x)\) is constant on \((a, b)\).
4.3.1 Increasing/Decreasing Behavior of Functions
We prove now that the sign of the derivative determines whether a function \(f(x)\) is increasing or decreasing. Recall that \(f(x)\) is
- Increasing on \((a, b)\) if \(f(x_{1}) < f(x_{2})\) for all \(x_{1}, x_{2} \in (a, b)\) such that \(x_{1} < x_{2}\)
- Decreasing on \((a, b)\) if \(f(x_{1}) > f(x_{2})\) for all \(x_{1}, x_{2} \in (a, b)\) such that \(x_{1} < x_{2}\)
We say that \(f\) is “nondecreasing” if
\[ f(x_1)\leq f(x_2)\text{ for }x_1\leq x_2 \]
“Nonincreasing” is defined similarly. In Theorem 2, if we assume that \(f'(x) \geq 0\) (instead of \(> 0\)), then \(f(x)\) is nondecreasing on \( (a, b)\). If \(f'(x) \leq 0\), then \(f(x)\) is nonincreasing on \((a, b)\).
We say that \(f(x)\) is monotonic on \((a, b)\) if it is either increasing or decreasing on \((a, b)\).
THEOREM 2 The Sign of the Derivative
Let \(f\) be a differentiable function on an open interval \((a, b)\).
- If \(f'(x) > 0\) for \(x \in (a, b)\), then \(f\) is increasing on \((a, b)\).
- If \(f'(x) < 0\) for\( x \in (a, b)\), then \(f\) is decreasing on \((a, b)\).
228
Proof
Suppose first that \(f'(x) > 0\) for all \(x \in (a, b)\). The MVT tells us that for any two points \(x_{1} < x_{2} \in (a, b)\), there exists \(c\) between \(x_{1}\) and \(x_{2}\) such that
\[f(x_{2}) - f(x_{1}) = f'(c)(x_{2} - x_{1}) > 0\]
The inequality holds because \(f'(c)\) and \((x_{2} - x_{1})\) are both positive. Therefore, \(f(x_{2}) > f(x_{1})\), as required. The case \(f'(x) < 0\) is similar.
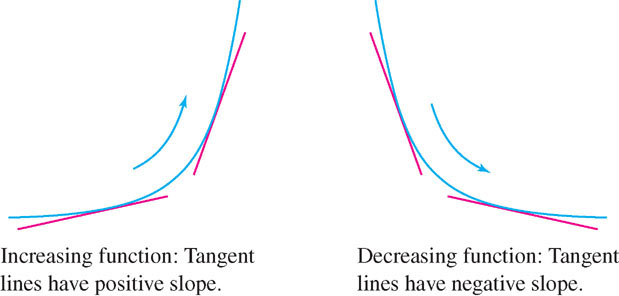
GRAPHICAL INSIGHT
Theorem 2 confirms our graphical intuition (Figure 4.26):
- \(f'(x)>0\implies\text{Tangent lines have positive slope}\implies f\text{ increasing}\)
- \(f'(x)<0\implies\text{Tangent lines have negative slope}\implies f\text{ decreasing}\)
EXAMPLE 2
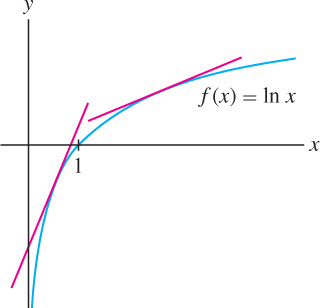
Show that \(f(x) = \ln x\) is increasing.
Solution The derivative \(f'(x) = x^{-1}\) is positive on the domain \(\{x : x \gt 0\}\), so \(f(x) = \ln x\) is increasing. Observe, however, that \(f'(x) = x^{-1}\) is decreasing, so the graph of \(f(x)\) grows flatter as \(x \rightarrow \infty\) (Figure 4.27).
EXAMPLE 3
Find the intervals on which \(f(x) = x^{2} - 2x - 3\) is monotonic.
Solution
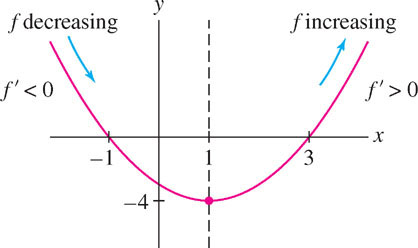
Question 4.7 Increasing/Decreasing Progress Check 1
UCHT24TI4pxq2FUnEY3WOYFHNQfxbN31NqEKxd4/0de68H00mPTD4jfkjb1yUH81SKaUdI2OO0pScDfhliMHd38tfsEfmWw3hSApX7+sKMCYTCBpZcQNpSdtmOce49Qqi5AL1Elss3LmzoC8Rtt/pHpo+MF8ryYiYNnSkd+mCL2jkJe5EgGQXkrg0EWvR8x2dCseu6yhyU9c8F22K1jU14hiT+D7kevR/ls6zW8YExTn8C5O1i3Vyify0id8qFNJ4.3.2 Testing Critical Points
There is a useful test for determining whether a critical point is a min or max (or neither) based on the sign change of the derivative \(f'(x)\).
229
To explain the term “sign change,” suppose that a function \(F(x)\) satisfies \(F(c) = 0\). We say that \(F(x)\) changes from positive to negative
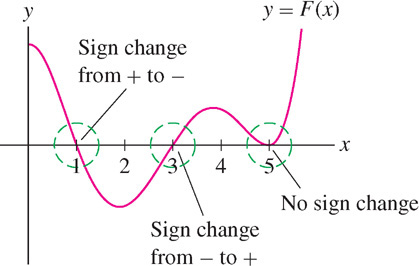
Now suppose that \(f'(c) = 0\) and that \(f'(x)\) changes sign at \(x = c\), say from \(+\) to \(-\). Then \(f(x)\) is increasing to the left of \(c\) and decreasing to the right, so \(f(c)\) is a local maximum. Similarly, if \(f'(x)\) changes sign from \(-\) to \(+\), then \(f(c)\) is a local minimum. See Figure 4.30(A).
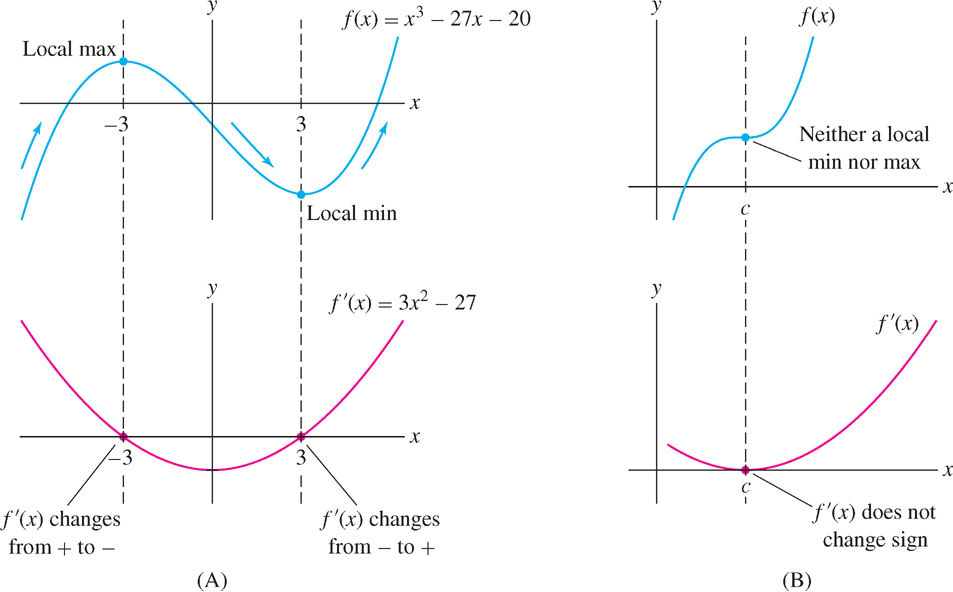
Figure 4.30(B) illustrates a case where \(f'(c) = 0\) but \(f'\) does not change sign. In this case, \(f'(x) > 0\) for all \(x\) near but not equal to \(c\), so \(f(x)\) is increasing and has neither a local min nor a local max at \(c\).
THEOREM 3 First Derivative Test for Critical Points
Assume that \(f(x)\) is differentiable and let \(c\) be a critical point of \(f(x)\). Then
- \(f'(x)\text{ changes from \(+\) to \(-\) at }c\implies f(c)\text{ is a local maximum.}\)
- \(f'(x)\text{ changes from \(-\) to \(+\) at }c\implies f(c)\text{ is a local minimum.}\)
To carry out the First Derivative Test, we make a useful observation: \(f'(x)\) can change sign at a critical point, but it cannot change sign on the interval between two consecutive critical points (one can prove this is true even if \(f'(x)\) is not assumed to be continuous). So we can determine the sign of \(f'(x)\) on an interval between consecutive critical points by evaluating \(f'(x)\) at an any test point \(x_{0}\) inside the interval. The sign of \(f'(x_{0})\) is the sign of \(f'(x)\) on the entire interval.
EXAMPLE 4
Analyze the critical points of \(f(x) = x^{3} - 27x - 20\).
Solution Our analysis will confirm the picture in Figure 4.30(A).
230
Step 1. Find the critical points.
\[ \text{The roots of }f'(x) = 3x^{2} - 27 = 3(x^{2} - 9) = 0\text{ are }c = \pm 3. \]
Step 2. Find the sign of \(f'\) on the intervals between the critical points.
The critical points \(c = \pm 3\) divide the real line into three intervals:
\[(-\infty,-3)\quad(-3,3)\quad(3,\infty)\]
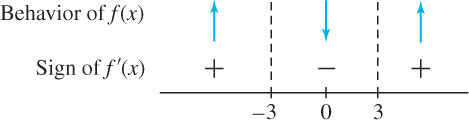
To determine the sign of \(f'\) on these intervals, we choose a test point inside each interval and evaluate. For example, in \((-\infty , -3)\) we choose \(x = -4\). Because \(f'(-4) = 21 > 0\), \(f'(x)\) is positive on the entire interval \((-3, \infty )\). Similarly,
We chose the test points -4, 0, and 4 arbitrarily. To find the sign of \(f'(x)\) on \( (-\infty , -3)\), we could just as well have computed \(f'(-5) \) or any other value of \(f' \) in the interval \( (-\infty , -3)\).
\begin{eqnarray*} f'(-4)&=&21>0&\implies&f'(x)>0&\text{for all }x\in(-\infty,-3)\\ f'(0)&=&-27<0&\implies&f'(x)<0&\text{for all }x\in(-3,3)\\ f'(4)&=&21>0&\implies&f'(x)>0&\text{for all }x\in(3,\infty) \end{eqnarray*}
This information is displayed in the following sign diagram:
Step 3. Use the First Derivative Test.
- \(c=-3:f'(x)\text{ changes from \(+\) to \(-\)}\implies f(-3)\text{ is a local max.}\)
- \(c=3:\phantom{-}f'(x)\text{ changes from \(-\) to \(+\)}\implies f(3)\phantom{-}\text{ is a local min.}\)
Question 4.8 Testing Critical Points Progress Check 1
Assume that \( f'(c)=0 \) and that \( f'(x) \) changes from + to - at the critical point \(x=c\). This means that \(f\) has oRyruCKfpgbZSBADYmGmAwKFtrVg19nqi9NV1zvtrjXS9F4AZ+muFhbnm1i82C+j7FTSdfxYPFtabv9VNoFC416F5OIlGD1d7jPX1WEsKHY= at \(x=c\).
Assume that \( f'(c)=0 \) and that \( f'(x) \) changes from - to + at the critical point \(x=c\). This means that \(f\) has Ny7bHD3WiA638S3N2WVgpAhW6b1z3d9HNeHKcRc1EGQ2I9BOFqcFaDBmskFyx3HC4dqOWU+QthsX9gd0rCL4Nhfl+ZfWs8sXIWsViBwsJdM= at \(x=c\).
EXAMPLE 5
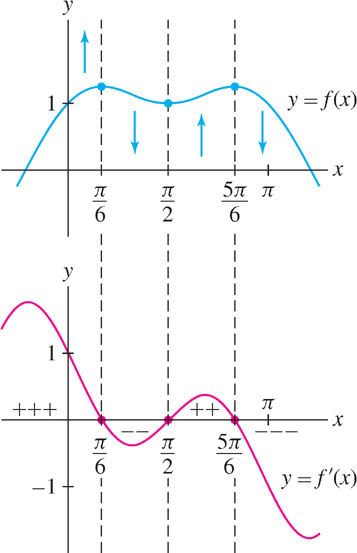
Analyze the critical points and the increase/decrease behavior of \(f(x) = \cos^{2}x + \sin x\) in \((0, \pi )\).
Solution First, find the critical points:
\[ f'(x) = -2\cos x\sin x+\cos x = (\cos x)(1-2\sin x) = 0 \implies\cos x=0\text{ or }\sin x=\frac{1}{2} \]
The critical points are \(\frac{\pi}{6}\), \(\frac{\pi}{2}\) and \(\frac{5\pi}{6}\). They divide \((0, \pi )\) into four intervals:
\[ \left(0,\frac{\pi}{6}\right)\quad \left(\frac{\pi}{6},\frac{\pi}{2}\right)\quad \left(\frac{\pi}{2},\frac{5\pi}{6}\right)\quad \left(\frac{5\pi}{6},\pi\right)\quad \]
We determine the sign of \(f'\) by evaluating \(f'\) at a test point inside each interval. Since \(\frac{\pi}{6}\approx0.52\), \(\frac{\pi}{2}\approx1.57\), \(\frac{5\pi}{6}\approx2.62\) and \(\pi\approx3.14\), we can use the following test points.
| Interval | Test Value | Sign of \(f'(x)\) | Behavior of \(f(x)\) |
|---|---|---|---|
| \(\left(0,\frac{\pi}{6}\right)\) | \(f'(0.5) \approx0.04\) | \(+\) | \(\uparrow\) |
| \(\left(\frac{\pi}{6},\frac{\pi}{2}\right)\) | \(f'(1) \approx-0.37\) | \(-\) | \(\downarrow\) |
| \(\left(\frac{\pi}{2},\frac{5\pi}{6}\right)\) | \(f'(2) \approx0.34\) | \(+\) | \(\uparrow\) |
| \(\left(\frac{5\pi}{6},\pi\right)\) | \(f'(3) \approx-0.71\) | \(-\) | \(\downarrow\) |
Now apply the First Derivative Test:
- Local max at \(c=\frac{\pi}{6}\) and \(c=\frac{5\pi}{6}\) because \(f'\) changes from \(+\) to \(-\).
- Local min at \(c=\frac{\pi}{2}\) because \(f'\) changes from \(-\) to \(+\).
The behavior of \(f(x)\) and \(f'(x)\) is reflected in the graphs in Figure 4.32.
Question 4.9 Testing Critical Points Progress Check 2
The function \(\displaystyle f(x) = x e^x \) has one critical point. Find and classify it.
\(f(x) \) has CeWbkgurGWX4BkvoZ2h1c3I4BDKgFLZkdXZmCPymxOHkrBGeTjov5T6dKGDmw/3TCotI7JGTrV5SCDbaHtTdKynF/LyNam3/JjXEwt5s1Tw= at the critical point \(c=\)UYinCekNO0E=.
231
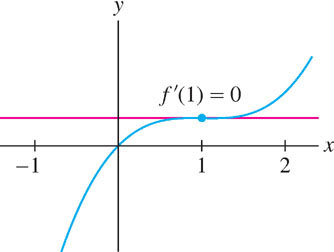
EXAMPLE 6 A Critical Point Without a Sign Transition
Analyze the critical points of \(f(x)=\frac{1}{3}x^3 - x^2 + x\).
Solution The derivative is \(f'(x) = x^{2} - 2x + 1 = (x - 1)^{2}\), so \(c = 1\) is the only critical point. However, \((x - 1)^{2} \geq 0\), so \(f'(x)\) does not change sign at \(c = 1\), and \(f(1)\) is neither a local min nor a local max (Figure 4.33).
Question 4.10 Testing Critical Points Progress Check 3
The function \(\displaystyle f(x) = -3x^4+8x^3-6x^2 \) has two critical points, \(c_1\) and \(c_2\). Find and classify them.
\(f(x) \) has x5yfWBjV/0cOg+BZDFy5N9/A1b+vbqTsK+V26DsDzMYcBcjzLrSZJtJfiSpJsHyOo5K4WGDaqpFYDo99U6kxMuVXlEUIigxy8Rmew6kUNCk= at the smaller critical point \(c_1=\)1Wh3cvJ2xF4=.
\(f(x) \) has ehsFOEG+56GC2dvJJ7SXJLl1CdTiQQhgIlAesvrZtFL5mJDuaQdWmH9g9C2/oZsLC0n3L/tld2IF3qddOm2HFN01ts7ag+reYoiRhRwpteI= at the larger critical point \(c_2=\)0VV1JcqyBrI=.
4.3.3 Proof of the MVT
Let \(m = \frac{f(b) - f(a)}{b-a}\) be the slope of the secant line joining \((a, f(a))\) and \((b, f(b))\). The secant line has equation \(y = mx + r\) for some \(r\) (Figure 4.34). The value of \(r\) is not important, but you can check that \(r = f(a) - ma\). Now consider the function
\[G(x) = f(x) - (mx + r)\]
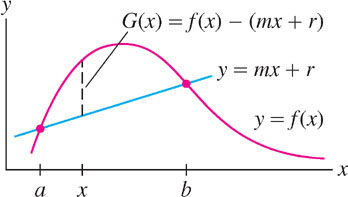
As indicated in Figure 4.34, \(G(x)\) is the vertical distance between the graph and the secant line at \(x\) (it is negative at points where the graph of \(f\) lies below the secant line). This distance is zero at the endpoints, and therefore \(G(a) = G(b) = 0\). By Rolle’s Theorem (Section 4.2), there exists a point \(c\) in \((a, b)\) such that \(G'(c) = 0\). But \(G'(x) = f'(x) - m\), so \(G'(c) = f'(c) - m = 0\), and \(f'(c) = m\) as desired.
4.3.4 Section 4.3 Summary
- The Mean Value Theorem (MVT): If \(f(x)\) is continuous on \([a, b]\) and differentiable on \((a, b)\), then there exists at least one value \(c\) in \((a, b)\) such that
\[ f'(c)=\frac{f(b) - f(a)}{b-a} \]
This conclusion can also be written
\[f(b) - f(a) = f' (c)(b - a)\]
- Important corollary of the MVT: If \(f'(x) = 0\) for all \(x \in (a, b)\), then \(f(x)\) is constant on \( (a, b)\), i.e. \(f(a_1)=f(a_2)\) for all \(a,b \in (a,b)\).
- The sign of \(f'(x)\) determines whether \(f(x)\) is increasing or decreasing:
\begin{eqnarray*} f'(x)>0\text{ for }x\in(a,b)&\implies&f\text{ is increasing on }(a,b)\\ f'(x)<0\text{ for }x\in(a,b)&\implies&f\text{ is decreasing on }(a,b)\\ \end{eqnarray*}
- The sign of \(f'(x)\) can change only at the critical points, so \(f(x)\) is monotonic (increasing or decreasing) on the intervals between the critical points.
- To find the sign of \(f'(x)\) on the interval between two critical points, calculate the sign of \(f'(x_{0})\) at any test point \(x_{0}\) in that interval.
- First Derivative Test: If \(f(x)\) is differentiable and \(c\) is a critical point, then
| Sign Change of \(f'\) - at \(c\) | Type of Critical Point |
|---|---|
| From \(+\) to \(-\) | Local maximum |
| From \(-\) to \(+\) | Local minimum |
232